M理论
在围棋游戏中,只有围与不围这样很少的几条规则,加上黑白两色棋子,却可以弈出千变万化的对局。与此相似,现代认为,自然界由很少的几条规则支配,而存在着无限多种这些支配规律容许的状态和结构。任何物理现象或者定律都只是这些规则的进一步推到与演化。那么对于其他事物而言,有没有可能也存在这种M理论呢?
社会契约论
我认为社会契约论算得上是社科的律法方面的一种M理论。初读社会契约论给我的感觉就是四个字:惊为天人。
社会契约论一共有四个章节,作者从原始部落到现代社会的形成逐步推演,向我们阐述社会的形成的过程与原理。论述了社会秩序和社会契约最原始的法律是从何而来,主权与权利的本质。在《社会契约论》中,卢梭主要阐述的命题就是:人人生而自由,却无处不在枷锁之中。这个枷锁就是国家。卢梭提出国家创建的理性逻辑:人类想要生存,个体的力量是微薄的,个人的权利、快乐和财产在一个有正规政府的社会比在一个无政府的、人人只顾自己的社会能够得到更好的保护,可行的办法就是集合起来,形成一个联合体,即国家。国家的目的就在于保护每个成员的人身与财产。国家只能是自由的人民自由协议的产物。人生而自由与平等,人们通过订立契约来建立国家,国家就是人民契约的结合体。有了这种公约和权利的保证,每个人对所有的人承担了义务,所有的人也对每一个人承担了义务,这就使得人与人之间虽然可能有体力与智力的不平等,但是他们却拥有了权利的平等。社科尚可通过严谨的逻辑推理而发现其本质特性,找到其中的M理论,那自然科学更应该可以通过逻辑推理获得其中的“M理论”了。
三次数学危机
数学无疑是一门高深的学科,但最初的数学也是很朴素的存在,正是经历了三次数学危机才让现在数学的“M理论”更加完善。第一次危机得到了无穷和无理数。最初人们对数学的认知还处在从自然数概念而形成有理数概念的早期阶段。当时的人们认为一切量都可以用有理数来表示,尤其是信仰“一切皆数”的毕达哥拉斯学派,深信数的和谐与数是万物的本源,宇宙间的一切现象都能归结为整数或整数比。在这样的背景条件下,毕达哥拉斯学派的希帕索斯发现了等腰直角三角形的直角边与斜边不可通约,这直接挑战了毕达哥拉斯学派的信条,冲击了古希腊人数学认知,引起了人们的恐慌,造成了数学上的第一次危机。最终由德国数学家戴德金才以有理数分割的理论结束了第一次数学危机,无理数正式纳入了数学体系当中。
第二次数学危机产生了微积分,本次数学危机是由一个叫做“芝诺的乌龟”数学悖论引出的,中国古书《庄子·天下篇》也有直白的描述:一尺之棰,日取其半,万世不竭。即把一根一尺长的木棍,每次截去一半,接着截取一半的一半,如此反复,虽然木棍在变短,但永远截不完。这个问题困扰了很多年,直到微积分的出现才被解决,这是一个关于无穷小求和的问题。但是事情并没有到此终结,上过高中的我们都学过微积分,牛顿和莱布尼茨两个人虽然都独自发明了微积分,但是他们对于无穷小的概念定义却相当的模糊。
当时的英国大主教贝克莱,他提出了贝克莱悖论:

这是一个求导的过程,我们知道分母不能为零,但是在最后的结果中△x又变为了0,简直是前后矛盾,最后由数学家柯西利用极限的方法精确定义了无穷小量的存在,才解决了这个危机。
第三次数学危机完善了数学“M理论”的基石——集合论。康托尔创立了著名的集合论。数学家们发现,从自然数与康托尔集合论出发可建立起整个数学大厦。因而集合论成为现代数学的基石,“一切数学成果可建立在集合论基础上”。然而这个时候天才数学家罗素又搞出来一个悖论:假如有这样一位理发师,他给自己定下了一个规矩:他只给不给自己刮胡子的人刮胡子,那么他应不应该给自己刮胡子呢。这个悖论是满足集合论的原理的,而且集合论现在已经深入到了数学的各个方面,如果这个悖论不解决,集合论就是有漏洞的。遗憾的是,至今为止,第三次数学危机也没有得到完美的解决,数学家哥德尔提出了不完备定律,证明了数学本身在理论上就是不完备的。
数学这种复杂的学科也是由简到难一步步构筑出宏大的“M理论”的,过程不可谓不漫长且艰辛。
康威生命游戏
康威生命游戏是一种用数字来模拟生命的游戏,我们有无限大的棋盘,棋盘中有很多方格,每个方格中都可放置一个生命细胞,每个生命细胞只有两种状态:“生”或“死”。用黑色方格表示该细胞为“生”,空格(白色)表示该细胞为“死”。或者说方格网中黑色部分表示某个时候某种“生命”的分布图。游戏开始时,每个细胞随机地设定为“生”或“死”之一的某个状态。然后,根据某种规则,计算出下一代每个细胞的状态,画出下一代细胞的生死分布图。计算规律:
- 当前细胞为死亡状态时,当周围有3个存活细胞时,则迭代后该细胞变成存活状态(模拟繁殖);若原先为生,则保持不变。
- 当前细胞为存活状态时,当周围的邻居细胞低于两个(不包含两个)存活时,该细胞变成死亡状态(模拟生命数量稀少)。
- 当前细胞为存活状态时,当周围有两个或3个存活细胞时,该细胞保持原样。
- 当前细胞为存活状态时,当周围有3个以上的存活细胞时,该细胞变成死亡状态(模拟生命数量过多)。
展示一个经典的动图:
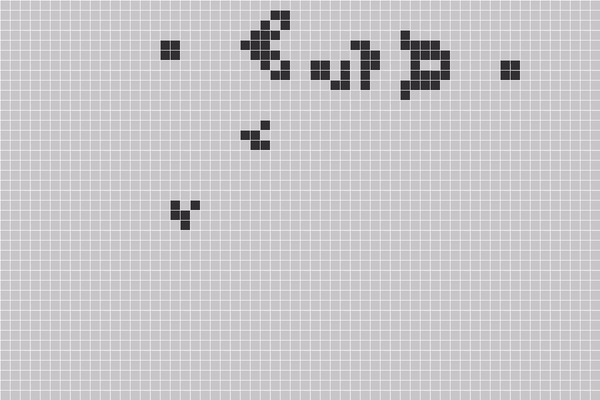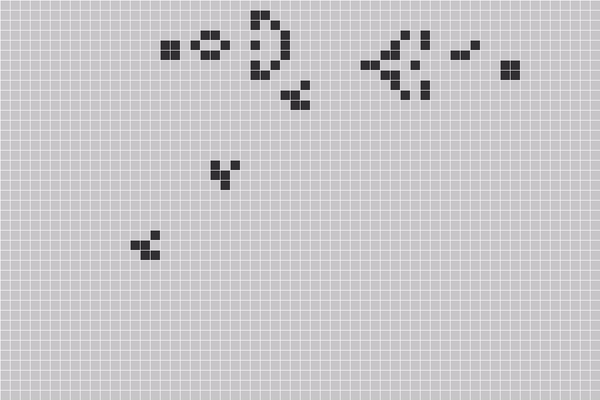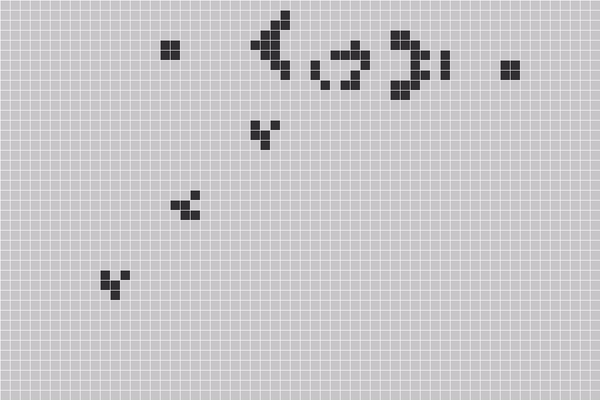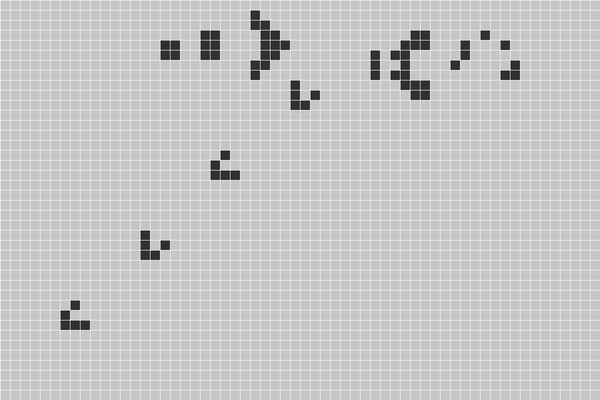
生命游戏中有一种结构叫做滑翔器发射器,它能够不停地复制某一个结构并将它发射出去,如同生命孕育之初的那一个单细胞生物。或许这就是生命中的”M理论”。
